mechanics – Softbites

2018-07-192018-07-19

Seeing Inside Sand: Visualizing Force Chains with Photoelastic Disks

As their name suggests, so-called “granular materials” are made up of “grains” — small (but macroscopic) pieces of sand, glass beads, coffee grounds, or almost any other solid you can think of. Granular materials can flow like a liquid (like sand in an hourglass), resist deformation like a solid (like the sand under your feet at the beach), or quickly transition between these states (like pebbles in a rockslide).

2017-12-062018-04-14

Dripping, Buckling and Collapsing of a Droplet

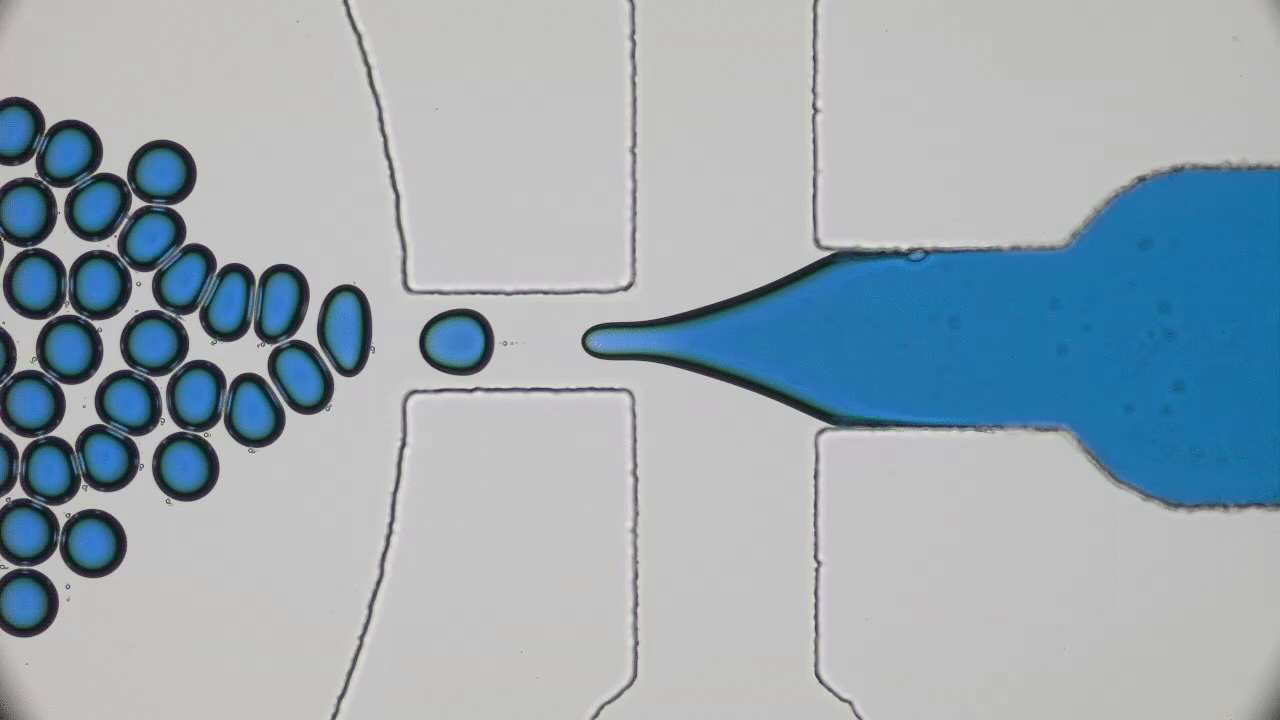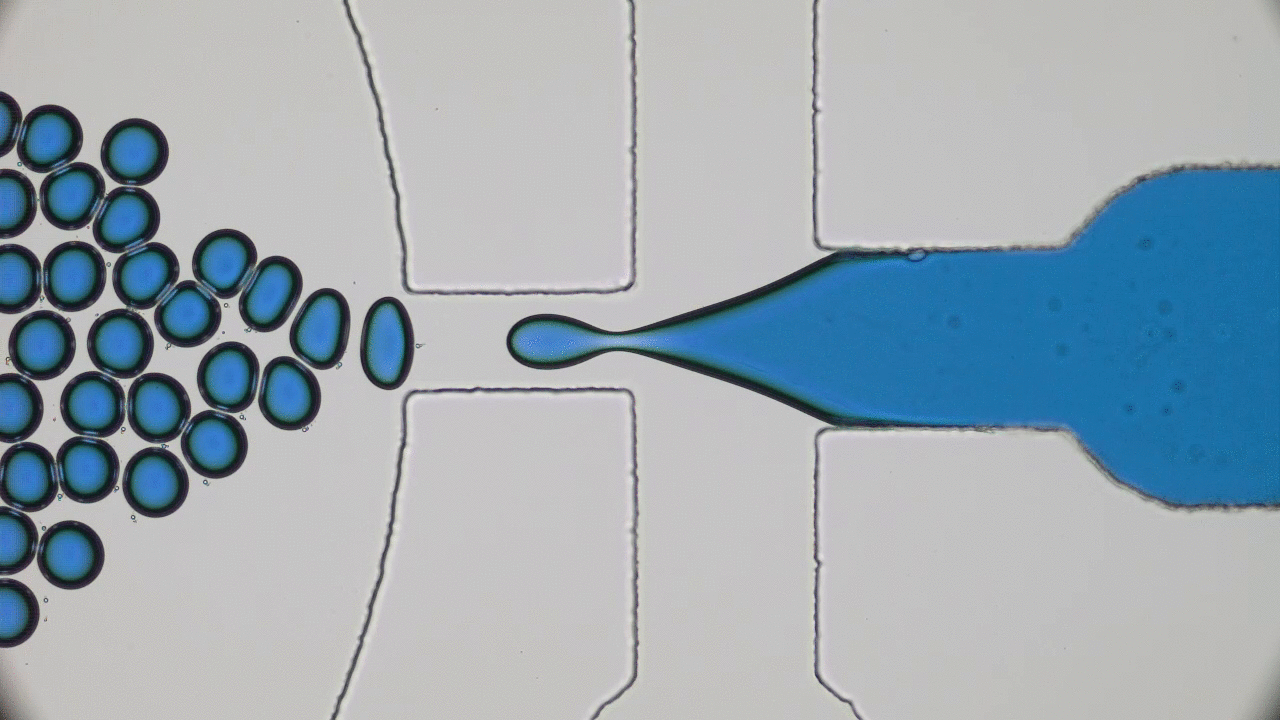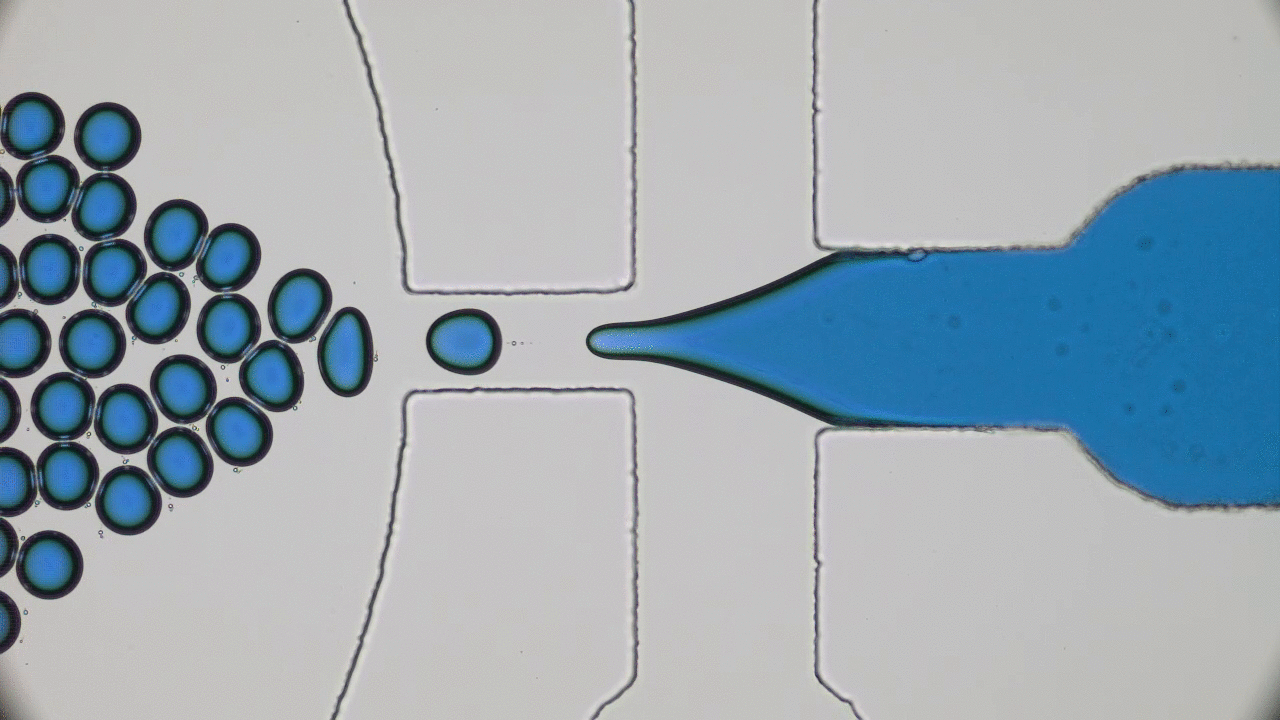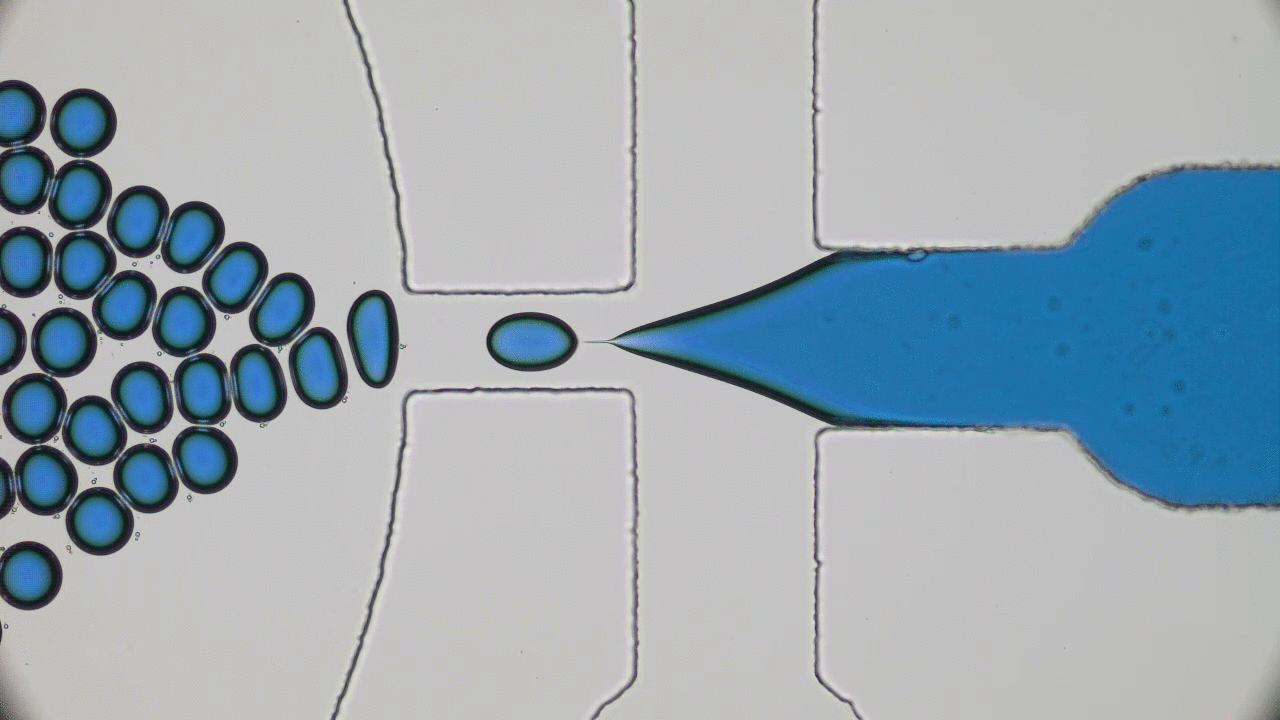
Cell membrane is evolved to be flexible rather than rigid. This fluid 2D sheet plays a key role in cells’s survival, be it tailoring the nutrition trafficking or rendering a mechanical toughness. In recent decades, however, artificial membranes have been developed with enhanced mechanical properties. Of such systems are particle-stabilized emulsions and in this post we will look into characterizing mechanical strength of such emulsion.